Résolution graphique de f(x)<k ou f(x)>k
Exemple :
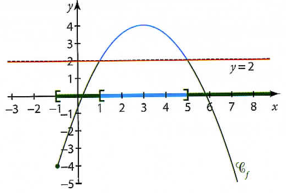
Résoudre \(f(x)<2\) puis \(f(x)>2\).
L'ensemble des solutions de :
\(f(x)<2\) est \([-1 ;1[ \cup ]5 ;+\infty[\) (la réunion d'intervalle en noir sur le schéma ci-dessous)
\(f(x)>2\) est \(]1 ;5[\) (en bleu ci-dessous, les bornes de l'intervalle étant exclues)
Méthode : Résolution de f(x) < k (resp. f(x)>k) par méthode graphique
On place k sur l'axe des ordonnées.
On repère tous les points de la courbe \(C_f\) d'ordonnée strictement inférieure (resp. supérieure) à k (donc situés sous la droite horizontal d'équation \(y=k\)).
On lit sur l'axe des abscisses les solutions de l'inéquation.
Attention : Attention au sens des crochets
On cherche une inégalité stricte. Les bornes 1 et 5 de l'intervalle pour lesquelles l'égalité \(f(x)=k\) est réalisée doivent être exclues.