Enroulement de la droite numérique
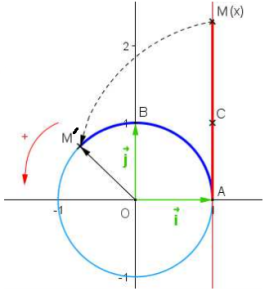
Dans un repère orthonormé \((O ;\vec i ;\vec j)\), on considère le cercle trigonométrique et une droite (AC) tangente au cercle en A et orientée telle que \((A ;\vec j)\) soit un repère de la droite.
Si l'on enroule la droite autour du cercle, on associe à tout point M d'abscisse x un point unique M' sur le cercle de manière à ce que la longueur de l'arc \(AM'\) soit égale à la longueur AM.
Animation
L'animation ci-dessous illustre le mécanisme d'enroulement.
Bouger le curseur t pour enrouler des points dans le sens direct (abscisses positives sur la droite)
Bouler le curseur s pour enrouler des points dans le sens indirect (abscisses négatives sur la droite)
Question
Par enroulement de la droite numérique, donner trois abscisses possibles du point M dont l'image sur le cercle est le point A de départ.
Indice
Le cercle trigonométrique a pour rayon 1 !
Solution
Le périmètre du cercle est \(2\pi\times R\) mais \(R=1\) donc le périmètre du cercle mesure \(2\pi\)
Par conséquent, voici trois abscisses possibles du point M dont l'image \(M'=A\)
M a pour abscisse 0
M a pour abscisse \(2\pi\) (on a fait un tour dans le sens direct)
M a pour abscisse -\(2\pi\) (on a fait un tour dans le sens indirect)
Plusieurs abscisses pour un même point
Ainsi à un point de la droite correspond un unique point sur le cercle.
Par contre, à un point du cercle (le point A dans l'exemple ci-dessus) peuvent correspondre une infinité de points de la droite ! En effet la droite peut s'enrouler une infinité de fois autour du cercle.
Question
On considère le point B du cercle trigonométrique de coordonnées (0 ;1). Donner Deux abscisses possibles d'un point M de la droite numérique s'enroulant sur le point B : une positive et une négative.
Quelle distance sépare ces deux abscisses possibles ?
Solution
Deux abscisses possibles
Le point B correspond à un quart de tour du cercle. Un tour faisant \(2\pi\), le point B correspond à un parcours dans le sens direct de \(\frac{2\pi}{4}\) soit \(\frac{\pi}{2}\)
Néanmoins on peut aussi parvenir au point B en parcourant 3 quart de tours dans le sens indirect, soit \(-\frac{3\pi}{2}\)
Deux abscisses possibles sont donc \(\frac{\pi}{2}\) et \(-\frac{3\pi}{2}\)
Distance entre ces abscisses
Ces deux abscisses sont séparées par une distance de \(\frac{\pi}{2}-\left(-\frac{3\pi}{2}\right)=2\pi\) soit un tour complet.
En général
De manière plus générale, Si un point M d'abscisse x s'enroule sur un point \(M'\) du cercle trigonométrique, tous les points d'abscisse \(x+2k\pi\) avec \(k\in\mathbb Z\) quelconque s'enrouleront aussi sur le même point \(M'\).
Les positions sur le cercle trigonométrique sont définies à \(2\pi\) près
Question
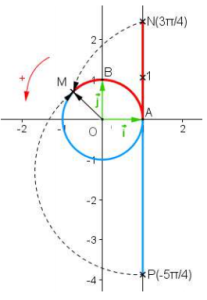
Soit M le point du cercle trigonométrique image du point N de la droite d'abscisse \(\frac{3\pi}{4}\)
On considère le point P d'abscisse négative le plus proche de N tel que P s'enroule également sur le point M.
Quelle est l'abscisse de P ?
Question
On enroule la droite orientée des réels sur le cercle trigonométrique de centre O.
Déterminer le point M du cercle associé au réel \(\frac{9\pi}{4}\) dans cet enroulement.
Solution
\(\frac{9\pi}{4}=\frac{8\pi}{4}+\frac{\pi}{4}=2\pi+\frac{\pi}{4}\)
L'enroulement effectué correspond à un tour complet du disque (\(2\pi\)) suivi d'un huitième de tour (\(\frac{\pi}{4}\))
Le point M se trouve donc sur le cercle trigonométrique tel que \(\widehat{AOM} = 45°\)
Question
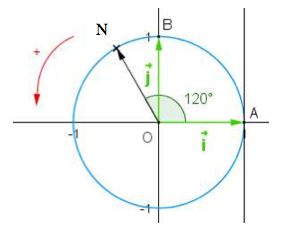
Placer sur le cercle trigonométrique le point N correspondants à l'angle 480°
Solution
480° = 360° + 120°.
Le point N se trouve donc sur le cercle trigonométrique tel que \(\widehat{AON} = 120°\) .