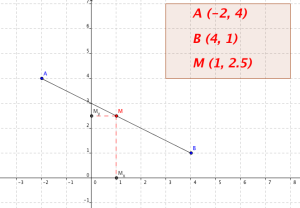
Coordonnées du milieu d'un segment
Rappel : Retour sur l'activité
Nous avons vu dans l'activité précédente que les coordonnées du milieu d'un segment semblaient s'obtenir par la demi-somme des coordonnées des extrémités du segment. En effet \(x_M=1=\frac{-2+4}{2}\) et \(y_M=2,5=\frac{4+1}{2}\).
Nous allons voir que cette supposition est effectivement vraie dans le cas général.
Fondamental : Coordonnées du milieu d'un segment
Dans un repère, on considère les points \(A(x_A ; y_A)\) et \(B(x_B ; y_B)\) et le point \(M(x_M ; y_M)\) milieu du segment \([AB]\).
Les coordonnées de M se calculent à partir de celles de A et B par la formule suivante :
\(x_M=\frac{x_A+x_B}{2}\)
\(y_M=\frac{y_A+y_B}{2}\)
Complément : Justification
Prenons le cas particulier de deux points A et B sur une droite graduée. La distance de A à M est égale à la distance de M à B.
La distance de A à M sur la droite est égale à \(x_M - x_A\) puisque M est entre A et B.
La distance de M à B sur la droite est égale à \(x_B - x_M\) puisque M est entre A et B.
Par conséquent on peut écrire \(x_M-x_A = x_B-x_M\). En ajoutant \(x_M+x_A\) aux deux membres de l'égalité on obtient
\(2\times x_M=x_A+x_B\). En divisant les deux membres de l'égalité par deux, cela donne :
\(x_M=\frac{x_A+x_B}{2}\).
En procédant de même sur l'axe des ordonnées dans le cas d'un repère du plan, on obtient bien la formule désirée.
Exemple :
Soit A(5 ;3) et B(-2 ;-6) dans un repère. Les coordonnées du milieu M du segment [AB] sont :
\(x_M=\frac{5+(-2)}{2}=1,5\) et \(y_M=\frac{3+(-6)}{2}=-1,5\)
donc M(1,5 ;-1,5).