Simuler le lancer d'un dé
Regarder la vidéo
On lance 30 fois un dé non truqué et on note le numéro obtenu.
Pour simuler le lancer d'un dé à la calculatrice, on peut utiliser la fonction RandInt(1,6) qui retourne un nombre aléatoire entier entre 1 et 6
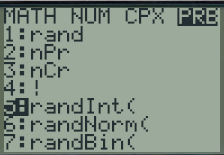
Sur TI la fonction se trouve sous la touche \(\fbox {math}\) puis \(\fbox {PRB}\) 5 :RandInt(
En appuyant successivement sur la touche \(\fbox{enter}\) on répète plusieurs fois l'expérience aléatoire.
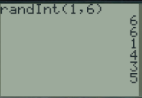

Sur Casio, la fonction RandInt n'existe pas. Il faudra la recréer à partir de la fonction \(\fbox{Ran\#}\) qui renvoie un réel entre 0 et 1.
Sachant 0<Ran# <1,
0<6*Ran# <6
1<6*Ran#+1<7
Et pour obtenir un nombre entier, on utilise la fonction Int(
Nous taperons donc Int (6*Ran#+1) pour simuler notre jeu de dé.
Sur Casio,
la fonction Int( se trouve dans \(\fbox{OPTN}\) \(\fbox{F6}\) \(\fbox{NUM}\) Int(
la fonction Ran# se trouve dans \(\fbox{OPTN}\) \(\fbox{F6}\) \(\fbox{PROB}\) Ran#
Question
A l'aide de la calculatrice, simuler 30 lancers et complétez le tableau suivant.
Face | 1 | 2 | 3 | 4 | 5 | 6 | Total |
|---|---|---|---|---|---|---|---|
Effectif | 30 | ||||||
Fréquence (décimal) | 1 | ||||||
Fréquence en pourcentage | 100 % |
Que remarquez-vous ? est-ce conforme à vos attentes ?
Solution
Face | 1 | 2 | 3 | 4 | 5 | 6 | Total |
|---|---|---|---|---|---|---|---|
Effectif | 4 | 7 | 5 | 5 | 8 | 1 | 30 |
Fréquence (décimal) | 0,13 | 0,23 | 0,16 | 0,16 | 0,27 | 0,03 | 1 |
Fréquence en pourcentage | 13% | 23% | 16% | 16% | 27% | 3% | 100 % |
On remarque sur cette expérience que le nombre d'apparition de chaque face n'est pas régulier. On pourrait s'attendre puisque le dé est équilibré à avoir chacune des faces représentée équitablement, donc autour de 16% d'apparition.
Question
Refaire l'expérience de 30 lancers 35 fois et cumuler les résultats obtenus.
On pourra pour cela demander à chaque élève de faire 30 fois l'expérience et additionner chaque effectif de chaque face.
Que remarque t-on ?
Solution
Face | 1 | 2 | 3 | 4 | 5 | 6 | Total |
|---|---|---|---|---|---|---|---|
Effectif | 168 | 191 | 169 | 190 | 167 | 165 | 1050 |
Fréquence (décimal) | 0,16 | 0,18 | 0,16 | 0,18 | 0,16 | 0,16 | 1 |
Fréquence en pourcentage | 16% | 18% | 16% | 18% | 16% | 16% | 100 % |
Sur cette nouvelle simulation comportant plus d'expériences, on remarque que les fréquences sont d'avantage regroupées autour des 16 % que l'on s'attend à trouver.
Loi des grands nombres
La loi des grands nombres est une loi qui permet d'affirmer que lorsqu'on répète une expérience aléatoire donnée un grand nombre de fois et de façon indépendante, la fréquence d'apparition de chaque issue se stabilise à une valeur donnée.
Cette valeur est égale à la probabilité de cette issue.
Nous allons nous intéresser dans la suite de ce chapitre au calcul de ces probabilités.