Fonction Inverse
Définition : Fonction inverse
La fonction définie sur \(]-\infty ;0[\cup]0 ;+\infty[\), qui à tout nombre réel \(x\) différent de 0 associe son inverse \(\frac{1}{x}\) est appelée fonction inverse.
Soit \(f\) cette fonction : \(f :x \longmapsto \frac{1}{x}\) ou \(f(x)=\frac{1}{x}\).
Méthode : Sens de variation de la fonction inverse
La fonction \(f :x \longmapsto \frac{1}{x}\) est décroissante sur \(]-\infty ;0[\) et décroissante \(]0 ;+\infty[\).
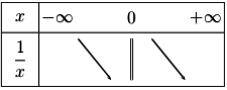
Ici, la double barre par convention signifie que la fonction n'est pas définie en \(x=0\).
Complément : Démonstration
Nous avons conjecturé ce résultat sur \(]0 ;+\infty[\). Nous allons à présent en faire une preuve algébrique.
Soient u et v deux réels tels que \(0<u<v\). On s'intéresse au signe de \(f(u)-f(v)\).
\(\frac{1}{u}-\frac{1}{v}=\dfrac{v-u}{uv}\)
Or u et v sont de même signe donc \(uv\) est positif d'après la règle des signes.
De plus u<v donc \(v-u\) est strictement positif. Le quotient de deux nombres positifs est positif.
Par conséquent \(f(u)-f(v)>0\) donc \(f(u)>f(v)\).
Donc f renverse donc le sens des inégalités. Elle est décroissante sur \(]0 ;+\infty[\).
La méthode et les calculs ci-dessus restent valables sur \(]-\infty ;0[\). Le résultat se généralise donc sur les réels négatifs.
Définition : Représentation graphique de la fonction inverse
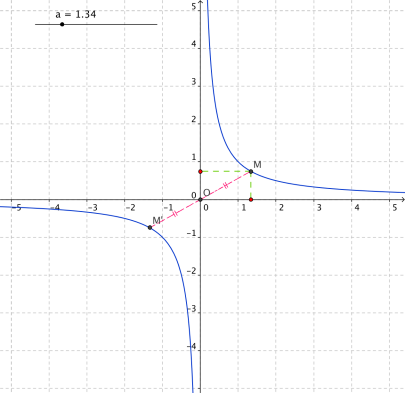
Dans un repère, la représentation graphique de la fonction inverse est appelée hyperbole.
Fondamental : Propriété de symétrie
Dans un repère d'origine O, l'hyperbole \(H\) représentant la fonction inverse est symétrique dans une symétrie centrale de centre le point O.
Complément :
En effet, soit \(M(x ;\frac{1}{x})\) un point de la courbe de la fonction inverse, alors le point \(M'(-x ;\frac{1}{-x})\) est également un point de la courbe.
Le milieu de [MM'] a pour coordonnées \((\frac{x-x}{2} ; \frac{\frac{1}{x}-\frac{1}{x}}{2})\). C'est donc \(O(0,0)\), l'origine du repère et ce pour tout nombre x réel non nul. Cela démontre la propriété de symétrie de la courbe.