On considère toujours le caractère d'hypertension qui apparaît avec une proportion de 0,3 dans la population, mais nous prenons à présent des échantillons de 100 personnes.
Question
Quel est l'intervalle de fluctuation correspondant à cette situation ?
Solution
Nous avons p=0,3, n=100. Les conditions de validité[1] de la formule sont respectées. Nous pouvons donc calculer l'intervalle de fluctuation au seuil de 95% à l'aide de la formule vue en cours.
\(I=\left[ 0,3-\frac{1}{\sqrt{100}} ;0,3+\frac{1}{\sqrt{100}}\right]\)
donc \(I=[0,2 ;0,4]\)
On peut donc s'attendre avec une probabilité de 0,95 que les fréquences observées dans les échantillons soient comprises entre 0,2 et 0,4
Question
Si on prend 500 échantillons différents de taille 100, à combien d'échantillons dont la fréquence observée du caractère se situe en dehors de l'intervalle de fluctuation calculé ci-dessus peut-on s'attendre ?
Solution
On a 5% de chances que les échantillons soient en dehors de l'intervalle de fluctuation. Sur 500 échantillons, on peut donc s'attendre à \(500\times \frac{5}{100}\) soit 25 échantillons en dehors de l'intervalle.
Remarque :
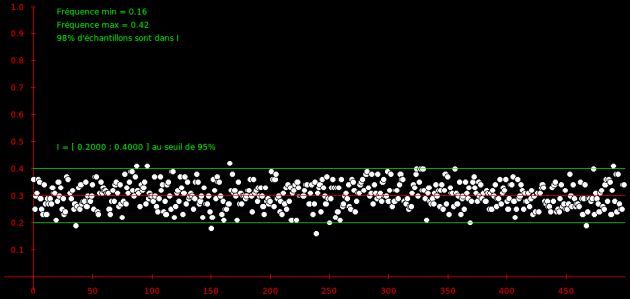
Ceci n'est bien sur qu'une probabilité. En pratique, sur une simulation de 500 échantillons, le nombre d'échantillons situés à l'intérieur de l'intervalle peut fluctuer autour de la probabilité de 95%. Sur la simulation ci-dessous par exemple, nous lisons que 98% des échantillons sont dans l'intervalle de fluctuation.