La fonction racine carrée
Définition : Fonction carré
La fonction définie sur \([0 ;+\infty[\), qui à tout nombre réel \(x\) positif associe sa racine carrée \(\sqrt x\), est appelée fonction racine carrée.
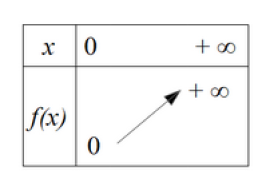
Fondamental : Propriété 1
La fonction \(f :x \longmapsto \sqrt x\) est strictement croissante sur l'intervalle \([0 ;+\infty[\).
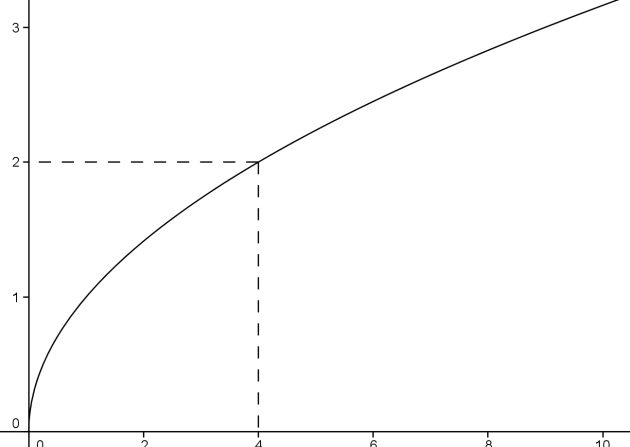
Définition : Représentation graphique
Dans un repère orthogonal d'origine O, la représentation graphique de la fonction racine carrée est une demi-parabole couchée :
Complément :
Soit f la fonction définie pour tout \(x∈[0;+∞[\) par \(f(x)=\sqrt x\).
On se propose d'établir le sens de variation de \(f\) sur \([0;+∞[\).
Pour tous nombres réels \(a∈[0;+∞[\) et \(b∈[0;+∞[\) tels que \(a>b\) :
\(f(a)−f(b)=\sqrt a−\sqrt b=\frac {(\sqrt a-\sqrt b) \times (\sqrt a+\sqrt b)} {\sqrt a+\sqrt b}=\frac{(\sqrt a) ²-(\sqrt b)²} {\sqrt a+\sqrt b}=\frac {a-b} {\sqrt a+\sqrt b}\).
Or le dénominateur \((\sqrt a+\sqrt b)\) est un nombre positif, et le numérateur est aussi positif. Il en résulte que \(f(a)-f(b)>0\) si \(a>b\).
La fonction racine carrée est donc strictement croissante sur son intervalle de définition.
Position relatives de trois courbes
Complément :
Pour justifier la position relative des courbes, on peut étudier les signes de :
\(x²-x\) en factorisant ;
\(x-\sqrt{x}\) en mettant \(\sqrt{x}\) en facteur : \(x-\sqrt{x}=\sqrt{x}(\sqrt{x}-1]\). Or \(\sqrt{x}>0\) et \(\sqrt{x}-1>0\) si et seulement si \(x>1\) car la fonction \(x \longmapsto \sqrt{x}\) est croissante.