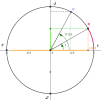
Cosinus et sinus d'un réel et d'un angle orienté
Soit M l'image d'un réel \(t\) sur le cercle trigonométrique.
Le cosinus de \(t\), noté \(cos\ t\) est l'abscisse du point M et le sinus de \(t\), noté \(sin \ t\), est l'ordonnée de M.
Fondamental : Propriété
Pour tout réel \(t\), \(cos^2 t+sin^2 t=1\)
Pour tout réel \(t\) :
\(-1\leq cos\ t \leq 1\), et
\(-1\leq sin\ t \leq 1\)
Pour tout réel \(t\), pour tout entier relatif \(k\) :
\(cos(t+k\times 2 \pi)=cos\ t\)
\(sin(t+k\times 2 \pi)=sin\ t\)
Complément : Définition
De part la propriété précédente, on peut définir le cosinus et le sinus d'un angle orienté comme le cosinus et le sinus de n'importe laquelle de ses mesures.
Fondamental : Propriété
Pour tout réel \(t\), on a :
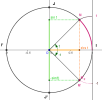
\(cos(-t) = cos (t)\)
\(sin(-t)=-sin(t)\)
Pour tout réel \(t\), on a :
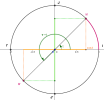
\(cos(\pi+t) = -cos (t)\)
\(sin(\pi+t)=-sin(t)\)
Pour tout réel \(t\), on a :
\(cos(\pi-t) = -cos (t)\)
\(sin(\pi-t)=sin(t)\)
Pour tout réel \(t\), on a :
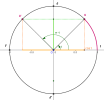
\(cos(\frac{\pi}{2}+t) = -sin (t)\)
\(sin(\frac{\pi}{2}+t))=cos(t)\)
Pour tout réel \(t\), on a :
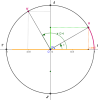
\(cos(\frac{\pi}{2}-t) = sin (t)\)
\(sin(\frac{\pi}{2}-t)=cos(t)\)
