Le couple (moyenne-écart-type)
Ce couple donne à la fois :
- Un indicateur de la tendance centrale de la série : la moyenne
- Un indicateur de dispersion faisant intervenir les carrés des écarts à la moyenne de toutes les
valeurs de la série.
Plus l'écart type est petit, plus les valeurs se concentrent autour de la moyenne.
Il joue un grand rôle en statistique théorique (par exemple appliqué au sondages). Les définitions
algébriques de la moyenne et de l'écart type se prêtent à des calculs algébriques permettant d'établir différentes propriétés.
Cependant l'écart type tient compte des écarts de toutes les valeurs à la moyenne. Il donne ainsi beaucoup de poids aux valeurs extrêmes, et son choix n'est pertinent que lorsque le diagramme qui représente la série est assez symétrique et évoque la forme d'une « courbe en cloche » comme ci-dessous.
Exemple : Courbe de Gauss « en cloche »
Un centre d'examen du baccalauréat a relevé les 600 notes obtenues, arrondies à l'entier supérieur, par des élèves de Première en enseignement scientifique.
Les résultats de ce relevé sont consignés dans le tableau suivant :
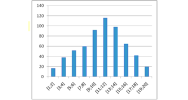
Représentons cette série statistique sous forme de « diagramme en bâtons » :
Cette répartition des notes a une forme particulière appelée « courbe en cloche » et est caractéristique d'une « distribution gaussienne ».
Remarque : Le terme « gaussien » vient du mathématicien allemand Frédéric Gauss (1777-1855).
Définition : On appellera distribution gaussienne toute répartition des données dont l'allure a cette forme de « courbe en cloche » ...