Démontrer une orthogonalité
Question
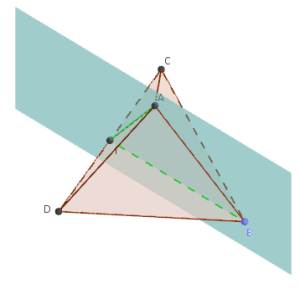
ABCD est un tétraèdre régulier.
Démontrer que les droites (CD) et (AB) sont orthogonales.
Indice
Dans un tétraèdre régulier, toutes les arrêtes sont de la même longueur.
Indice
On pourra construire le point I milieu de [CD]
Solution
Méthode : 1ère méthode : A l'aide du plan médiateur
AC=AD donc A appartient au plan médiateur de [CD],
BC=BD donc B appartient au plan médiateur de [CD],
IC=ID donc I appartient au plan médiateur de [CD].
De plus A, B et I ne sont pas alignés donc ils définissent un plan : c'est le plan médiateur de [CD].
Le plan ABI est donc orthogonal à la droite CD et donc toute droite de ce plan médiateur est orthogonale à (CD), donc en particulier (AB).
(AB) et (CD) sont donc orthogonales.
Méthode : 2ème méthode : Montrer que (CD) orthogonale à (ABI)
Dans le triangle équilatéral ADC, la médiane (AI) est aussi la hauteur issue de A donc \((CD)\bot(AI)\).
De même dans le triangle équilatéral BCD, \((CD)\bot(BI)\).
Donc (AI) et (BI) sont deux droites sécantes du plan (ABI) qui sont toutes deux perpendiculaires à (CD).
Par conséquent le plan (ABI) est orthogonal à la droite (CD).
Donc (AB) est orthogonale à (CD).