Vers la notion de primitive d'une fonction
Soit a et b deux réels et f une fonction continue et positive sur l'intervalle \([a ;b]\). \(\mathcal C\) désigne sa courbe représentative dans un repère orthogonal (O,I,J).
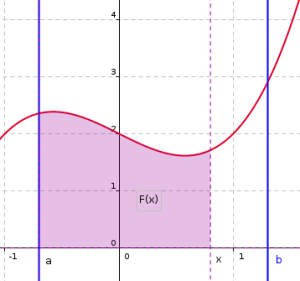
Pour tout réel \(x\in[a ;b]\), on peut définir la fonction \(F(x)=\displaystyle \int_a^x f(t)~dt\) comme étant l'aire sous la courbe \(\mathcal C\) sur l'intervalle \([a;x]\).
Remarque :
La fonction F est définie sur [a ;b] et :
\(F(a)=0\) puisque l'aire sur un domaine de largeur nulle est nulle.
\(F(b)= \displaystyle \int_a^b f(t)~dt\).
Exemple :
Reprenons l'exemple précédent : \(f :x\longmapsto -\dfrac{1}{2}x+5\).
On a alors \(F(x)=\displaystyle \int_{-1}^x -\dfrac{1}{2}t+5~dt\)
Si on utilise la méthode de l'aire du trapèze pour calculer cette intégrale, nous avons :
\(\mathcal{A}=\dfrac{(f(x)+5,5)}{2}\times (x+1)=(-\dfrac{x}{2}+5+5,5)\times \dfrac{x+1}{2}\)
\(\mathcal A=-\dfrac{x^2}{4}+\dfrac{10,5x}{2}-\dfrac{x}{4}+\dfrac{10,5}{2}\)
\(\mathcal A=-\dfrac{x^2}{4}+5x+5,25\)
On vérifie que :
\(F(-1)=-0,25-5+5,25=0\)
et
\(F(3)=-2,25+15+5,25=18\) ce qui est l'aire obtenue à l'exercice précédent.
Remarque : Avec l'exemple précédent,
On remarque à ce stade que si \(f(x)\) est une fonction affine, \(F(x)\) est un polynôme du second degré.
Une surprise nous attend si on calcule \(F'(x)\) : \(F'(x)=-\dfrac{x}{2}+5=f(x)\) ! ! ! !
Ce résultat n'est pas le fruit du hasard mais se généralise au moyen de la propriété suivante :
Fondamental : Théorème admis dans le cas général
Soit a et b deux réels et f une fonction continue et positive sur l'intervalle \([a ;b]\).
La fonction \(F(x)=\displaystyle \int_a^x f(t)~dt\) est dérivable sur \([a ;b]\), a pour dérivée \(f\) et s'annule pour \(x=a\).
Complément :
Pour calculer l'intégrale \( \displaystyle \int_a^b f(t)~dt\), il suffit de connaître une fonction F dérivable dont la dérivée est \(f\). Nous aurons alors :
\( \displaystyle \int_a^b f(t)~dt=F(b)-F(a)\).