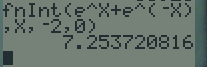Positivité
Fondamental : Propriété de positivité
Soit f une fonction continue positive sur un intervalle \([a ;b]\).
Alors \(\displaystyle \int_a^b f(x)~dx \geqslant 0\)
En d'autre termes, l'intégrale d'une fonction positive sur un intervalle est positive, ce qui est logique dans la mesure où elle s'interprète comme une aire (voir le début du cours).
Complément : Démonstration
Soit \(F\) une primitive de \(f\).
La fonction F est croissante car sa dérivée \(f\) est positive !
\(F\) conserve donc les inégalités. Puisque \(b\geqslant a,~ F(b) \geqslant F(a)\) donc \(\displaystyle \int_a^b f(x)~dx =F(b)-F(a)\geqslant 0\)
De cette propriété se déduit la suivante :
Fondamental : L'intégrale conserve les inégalités des fonctions.
Soit \(f\) et \(g\) deux fonctions continues sur un intervalle \([a ;b].\)
Si pour tout \(x\in [a ;b],~f(x)\leqslant g(x)\), alors \(\displaystyle \int_a^b f(x)~ dx \leqslant \displaystyle \int_a^b g(x)~ dx\)
Complément :
Cette propriété se démontre en utilisant la propriété de positivité sur la fonction \(g(x)-f(x)\) qui est positive.
Exemple :
Déterminer sans calculatrice le signe de \(\displaystyle \int_{-2}^0 e^x+e^{-x}~ dx\)
\(e^x\) et \(e^{-x}\) sont toutes deux positives sur\( [-2 ;0]\) donc puisque \(-2<0,~ \displaystyle \int_{-2}^0 e^x+e^{-x}~ dx>0\)
On peut faire une vérification à l'aide de la calculatrice.