Recherche d'un extremum
On considère la fonction f définie sur \(\mathbb{R}\) par \(f(x)=x^2+4x+1\).
Question
En utilisant la calculatrice, conjecturer l'existence d'un extremum de f sur \(\mathbb{R}\).
Indice
On pourra tracer la courbe représentative de f et en déduire le tableau de variation de f.
Solution
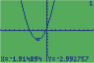
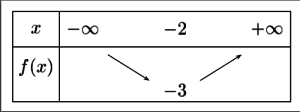
La calculatrice fournit le graphique suivant. On peut conjecturer que a fonction est décroissante jusqu'à x=-2 puis croissante.
On peut calculer que f(-2)=-3.
On peut dès lors dresser le tableau de variations suivant :
La fonction change de sens de variation. On en déduit la présence d'un extremum. Elle est décroissante puis croissante, c'est donc un minimum atteint en x=-2 qui semble être représenté par la calculatrice.
Question
Démontrer par le calcul cette conjecture.
Indice
On pourra étudier le signe de f(x)-f(-2).
Indice
Essayez la première égalité remarquable pour factoriser f(x)-f(-2)...
Solution
\(f(x)-f(-2)=x^2+4x+1-(-3)=x^2+4x+4=(x+2)^2\) d'après la première égalité remarquable.
Or un carré est toujours positif donc \(f(x)-f(-2) \geq 0\) pour tout réel x. C'est donc dire que f(x) est toujours plus grand que f(-2). Nous avons donc démontré que -3 est le minimum de la fonction f atteint en x=-2.