Dénombrer avec un arbre
L'expérience consiste à lancer trois fois une pièce de monnaie. On note le résultat sous la forme de trois lettres indiquant le résultat de chacun des trois tirages (par exemple, FPF signifie que l'on a obtenu face au premier tirage, pile au second et face au troisième).
On modélise cette situation où on réalise plusieurs expériences successives par un ≪ arbre ≫
Question
Modéliser cette expérience à l'aide d'un arbre.
Quelle est la probabilité de chaque issue ?
Solution
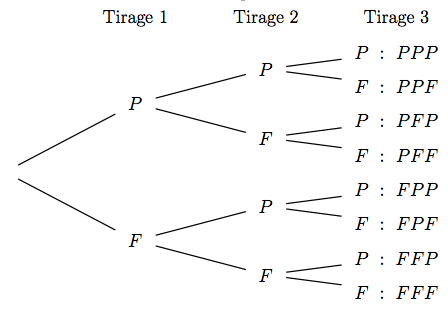
La probabilité sur chaque feuille est le produit des probabilités sur le chemin donc pour chacune on a \(\dfrac{1}{2}\times \dfrac{1}{2}\times \dfrac{1}{2}=\dfrac{1}{8}\)
Question
Décrire sous forme d'un ensemble l'événement A : « obtenir deux Piles exactement »
.
Calculer \(\mathbb P(A)\)
Indice
On pourra remarquer que puisque la pièce est équilibrée, chaque probabilité sur chaque branche vaut 1/2. Les issues de l'expérience sont donc équiprobables.
Solution
A={ PPF ;PFP ;FPP}
On est en situation d'équiprobabilité donc \(\mathbb P(A)=\dfrac{3}{8}\)
Question
On considère l'événement B : « obtenir au moins un Pile »
Décrire par un ensemble l'événement \(\bar B\)
En déduire la probabilité de l'événement B.
Solution
\(\bar B\) est l'événement « n'obtenir aucun Pile »
. Donc B={FFF}.
\(\mathbb P(\bar B)=\dfrac{1}{8} ~\text{donc}~ \mathbb P(B)=1-\dfrac{1}{8}=\dfrac{7}{8}\)