Signe de ax+b
Pour étudier le signe de \(f(x)=ax+b\) où \(a\neq0\), on est amené à distinguer deux cas selon le signe de a. En effet, du signe de \(a\) va dépendre la croissance ou la décroissance de la fonction.
Fondamental : Cas 1 : a<0
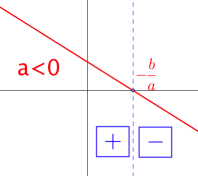
Si \(a < 0\), alors :
pour tout x de \(]-\infty ;-\frac{b}{a}[\), \(f(x)=ax+b>0\)
pour tout x de \(]-\frac{b}{a} ; +\infty[\), \(f(x)=ax+b<0\)
La valeur \(-\dfrac{b}{a}\) est tout simplement la "racine" de \(ax+b\), c'est-à-dire la valeur qui l'annule : c'est la solution de \(ax+b=0\) qu'il suffit de résoudre. On appelle ce nombre valeur charnière.
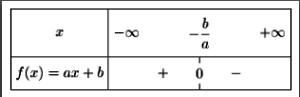
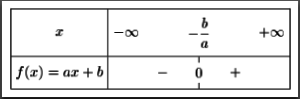
Ce qui peut se résumer grâce à l'emploi d'un tableau de signes :
Fondamental : Cas 2 : a>0
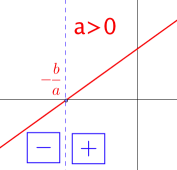
Si \(a > 0\), alors :
pour tout x de \(]-\infty ;-\frac{b}{a}[\) \(f(x)=ax+b<0\)
pour tout x de \(]-\frac{b}{a} ; +\infty[\) \(f(x)=ax+b>0\)
Ce qui peut se résumer grâce à l'emploi d'un tableau de signes :