Définition d'un angle orienté et mesure principale
Définition :
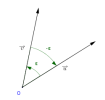
Soient \(\overrightarrow{u}\) et \(\overrightarrow{v}\) deux vecteurs non nuls.
Soient \(M\) et \(N\) les points tels que \(\overrightarrow{OM}=\overrightarrow{u}\) et \(\overrightarrow{ON}=\overrightarrow{v}\) et M' et N' tels que \(\overrightarrow{OM'}=\frac{\overrightarrow{OM}}{||\overrightarrow{OM}||}\) et \(\overrightarrow{ON'}=\frac{\overrightarrow{ON}}{||\overrightarrow{ON}||}\).
Soient \(M'\) et \(N'\) sont les images sur le cercle trigonométrique des réels \(t\) et \(t'\).
Alors l'angle orienté \((\overrightarrow{u} ;\overrightarrow{v})\) a pour mesure en radians \(t'-t\).
Fondamental : Propriété et définition
Un angle orienté a une infinité de mesures, mais une seule d'entre elles, nommée \(\alpha\) est dans l'intervalle \(]-\pi ;\pi]\) et les autres mesures sont de la forme \(\alpha+k\times 2\pi\), \(k \in \mathbb{Z}\).
On note :
\((\overrightarrow{u} ;\overrightarrow{v})=\alpha+k\times2\pi \ \ (k \in\mathbb{Z})\)
ou encore \((\overrightarrow{u} ;\overrightarrow{v})=\alpha\text{ modulo }2\pi\)
ou \((\overrightarrow{u} ;\overrightarrow{v})=\alpha\ \ [2\pi]\)
Si M, O, et N sont 3 points distincts, \(\widehat{MON}=|\alpha|\), où \(\alpha\) est la mesure principale de (\(\overrightarrow{OM}\);\(\overrightarrow{ON}\)).
Exemple :
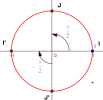
\((\overrightarrow{OI} ;\overrightarrow{OJ})=\frac{\pi}{2}+k\times 2\pi,\ (k \in \mathbb{Z})\)
\((\overrightarrow{OJ'} ;\overrightarrow{OI'})=-\frac{\pi}{2}+k\times 2\pi,\ (k\in \mathbb{Z})\)
Si \(\overrightarrow{u}\) et \(\overrightarrow{v}\) sont deux vecteurs non nuls, alors :
\((\overrightarrow{v},\overrightarrow{u})=-\ (\overrightarrow{u},\overrightarrow{v}) \text{ (modulo } 2\pi)\)
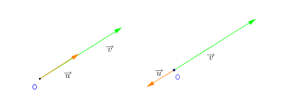
Si \(\overrightarrow{u}\) et \(\overrightarrow{v}\) sont deux vecteurs colinéaires et non nuls, alors :
\((\overrightarrow{u},\overrightarrow{v})=0\text{ ou }\pi \text{ (modulo } 2\pi)\)
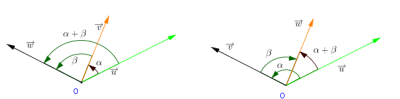
Si \(\overrightarrow{u}\), \(\overrightarrow{v}\) et \(\overrightarrow{w}\) sont des vecteurs non nuls, alors :
\((\overrightarrow{u},\overrightarrow{v})+(\overrightarrow{v},\overrightarrow{w})= (\overrightarrow{u},\overrightarrow{w})\text{ (modulo } 2\pi)\)