Fluctuation d'échantillonnage
Revenons à notre exemple de départ sur l'hypertension. Voici quelques exemples de fréquences observées dans des échantillons de 30 personnes :
;
;
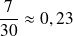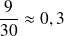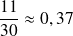etc...
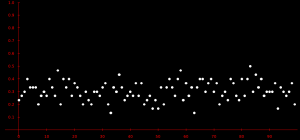
On constate que certaines fréquences sont égales à 0,3, mais pas toutes. Ces fréquences fluctuent autour de 0,3, on dit qu'il y a fluctuation d'échantillonnage.
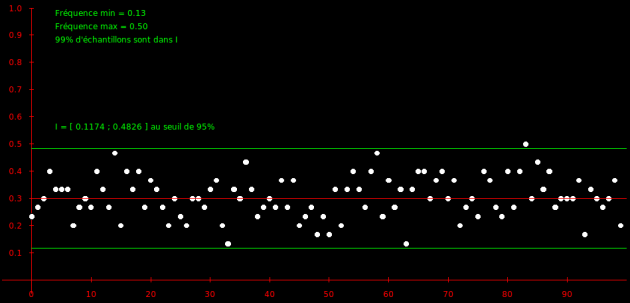
Le graphique ci-contre montre la simulation sur 100 échantillons de 30 personnes de la variation de la fréquence observée d'hypertendus. |  |
En fait, en théorie des probabilités, on démontre la propriété ci-dessous :
Fondamental : Intervalle de fluctuation au seuil de 95%
On considère un caractère apparaissant avec une proportion p dans une population.
On observe ce caractère dans un échantillon de taille n.
Sous certaines conditions[1], la fréquence f observée du caractère dans cet échantillon appartient à l'intervalle
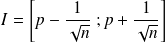avec une probabilité d'au moins 95%.
L'intervalle ci-dessus s'appelle l'intervalle de fluctuation au seuil 95 %.
